기술 문서자료
[설계]복잡한 설계 변수, Latin Hypercube Sampling으로 해결하세요!
- 25-07-08 00:00
- 웹스시스템코리아
설계자라면 누구나 이런 고민을 해본 적이 있을 것이다.
"설계를 할 때 매번 변수 조합을 어떻게 결정해야 하지?"
"가능한 모든 조건을 테스트할 수는 없는데, 어떻게 하면 효과적으로 변수를 선택할 수 있을까?"
이런 고민이 들 때마다 설계자들은 여러가지 방법을 고민하게 된다. 하지만 현실적으로 모든 경우의 수를 하나하나 테스트하는 것은 거의 불가능에 가깝다. 이때 효과적인 방법이 있는데, 바로 Latin Hypercube Sampling(LHS) 기법이다.
Latin Hypercube Sampling(LHS)의 기술적 원리와 특징
Latin Hypercube Sampling은 통계적 샘플링 기법 중 하나로, Monte Carlo 기법의 변형이다. 일반적인 무작위(Random) 샘플링이 설계 공간의 특정 영역에 데이터가 집중되는 경우가 많은데 비해, LHS는 설계 공간 전체를 균등하게 나누고, 각 구간에서 하나의 값을 선택하여 샘플을 생성한다. 즉, LHS는 설계 변수를 다음과 같은 방법으로 선정한다.
LHS의 기본적인 작동 원리
1. 설계 변수의 범위를 동일한 확률 간격으로 나눈다. 예를 들어, 설계 변수가 0 ~ 100까지 있다고 가정하면, 10개의 샘플을 얻기 위해 10개의 구간 [0-10), [10-20), [20-30), ... , [90-100] 으로 나눈다.2. 각 구간에서 무작위로 하나의 값을 샘플링 한다. 각 구간에서 추출된 값은 구간 전체를 대표하게 된다. 이렇게 하면 설계 공간 전체가 균형 잡힌 방식으로 고르게 선택된다.
3. 여러 변수가 있을 경우, 구간 선택이 독립적으로 진행된다. 따라서 모든 변수가 서로 독립적으로 균등하게 분포된 샘플을 확보할 수 있다.
LHS의 수학적 특징과 장점
-표본 효율성 (Sample Efficiency) - LHS는 Monte Carlo 대비 적은 샘플 수로 설계 공간을 균등히 탐색할 수 있어, 최소한의 시뮬레이션 또는 실험만으로 효과적인 결과를 얻을 수 있다.-균일성 (Uniformity) 보장 - 설계 변수를 구간별로 균일하게 선택하기 때문에, 설계 변수 간의 상호작용 효과도 효과적으로 포착 가능하다.
-분산 감소 (Variance Reduction) - 통계적으로 LHS는 일반 무작위 샘플링보다 더 낮은 분산을 나타내므로, 결과의 정확성과 신뢰성이 향상된다.
왜 설계 최적화에 LHS가 효과적일까?
설계 최적화는 일반적으로 많은 설계 변수와 복잡한 관계를 가지고 있다. 이때 무작위 샘플링으로는 충분한 정보를 얻기 위해 지나치게 많은 샘플이 필요하게 된다. 반면, LHS는 각 변수의 전체 범위를 적은 수의 샘플로 균등히 대표하여 효율적이고 정확한 데이터를 얻을 수 있다.
SmartSIM은 LHS를 어떻게 활용할까?
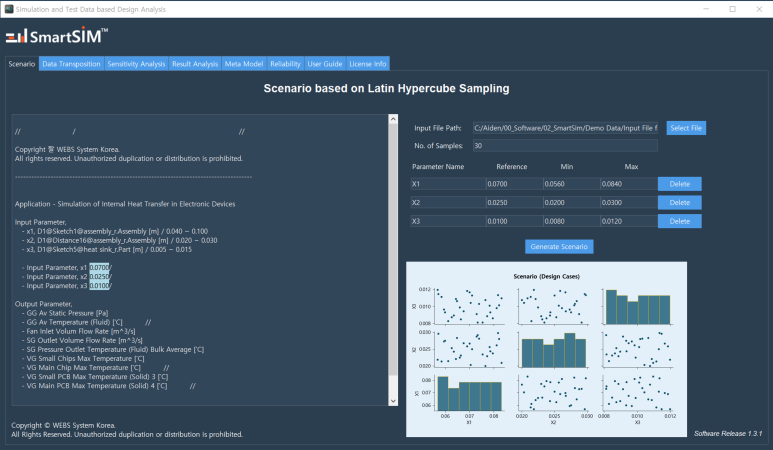
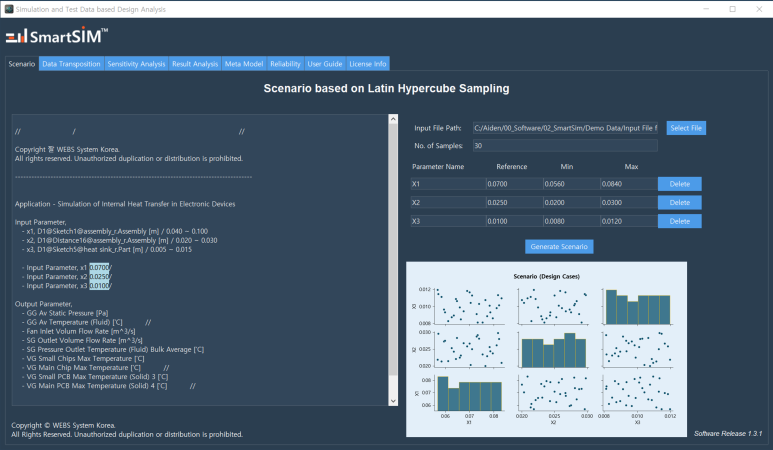
SmartSIM은 이 기술적 특징을 그대로 활용하여, 설계자가 변수 범위만 설정하면 즉시 LHS를 기반으로 자동으로 균등하고 효율적인 설계 시나리오를 생성한다. 이러한 방식은 결과적으로 다음과 같은 실제적인 이점을 제공한다.
-적은 시뮬레이션으로 최대의 정보를 얻음-데이터의 대표성과 신뢰성이 뛰어남
-변수 조합 선정의 고민을 해소하고, 데이터 분석과 의사결정 과정까지 가속화함